Cees J. van Westen,

International Institute for Aerospace Surveys and Earth Sciences (ITC).

PO Box 6, 7500 AA Enschede, The Netherlands. Tel.: 31.53.4874263 - fax: 31.53.4874336

ABSTRACT

Slope instability hazard assessment is based on the analysis of the terrain conditions at sites where slope failures occurred in the past. For the analysis of the causative factors the application of geographic information systems (GIS) is an essential tool in the data analysis and the subsequent hazard assessment. Three scale levels of hazard mapping are defined. A direct experience-driven mapping at reconnaissance level, a statistical approach to determine the causative factors in a quantitative susceptibility mapping and a methodology at large scale making use of deterministic models.

The occurrence of Natural Hazards is a serious constraint on economic development, particularly in developing countries, where the economic loss due to the impact of natural hazards often makes the difference between economic growth and stagnation (Fournier d'Albe,1976; Swiss Reinsurance Company, 1990). On the other hand practice has shown that adequate hazard mitigation is possible. The successful earthquake mitigation in the western United States in comparison to the earthquake in Armenia (1988), which had a comparable magnitude, is a striking example. Also successful examples of mitigation exist for other types of natural hazards (hurricane Andrew, Pinatubo volcano, etc.).

The present article presents the outlines of a methodology for landslide hazard zonation at small scales for regional assessments, medium scales for feasibility studies and large scales for local more detailed studies. The results, based on research in the Andean Cordillera in Colombia, are clarifying some of the methodological concepts.

Slope instability hazard zonation is defined as the mapping of areas with an equal probability of occurrence of landslides within a specified period of time (Varnes, 1984). A landslide hazard zonation consists of two different aspects:

• the assessment of the susceptibility of the terrain for a slope failure, in which the susceptibility of the terrain for a hazardous process expresses the likelihood that such a phenomenon occurs under the given terrain conditions or parameters.
• the determination of the probability that a triggering event occurs. The probability for the occurrence of a landslide is mostly evaluated by calculating the probability of triggering events, such as major rainfall events or earthquakes. It is important to mention here that the calculation of landslide probability is more difficult than for other natural disasters (such as floods or earthquakes) since there is no simple relation between the magnitude of a landslide event and a return period. Another complicating factor is that mostly there are no reliable historic records of landslides that allow to make a relation between landslide dates and rainfall or earthquakes.

An area is declared to be susceptible for landslides, when the terrain conditions at that site are comparable to those in an area where a slide has occurred. The instability of a slope is governed by a complex of normally interrelated terrain parameters, such as: lithology and the structural conditions of the rocks, the weathering and the contact with overlying soils, the properties of these soils, slope gradient and form, hydrological conditions, vegetation, land use and land use practice and finally human activities acting on the slope conditions.

The joint analysis of all these terrain variables in relation to the spatial distribution of landslides, has gained enormously by the introduction of Geographic Information Systems (GIS), the ideal tool for the analysis of parameters with a high degree of spatial variability.

Considering that for a slope instability hazard assessment the assumption is made that conditions which led in the past to slope failures, will also result in potential unstable conditions in the present, defines automatically the essential steps to be followed in a landslide susceptibility zoning, which are:

• a landslide distribution mapping, differentiating according type, activity, dimensions, etc. and based on information covering when possible a time span as large as possible,
• a mapping of the most relevant terrain parameters related to the occurrence of landslides,
• the analysis of the terrain conditions which can be considered responsible for the occurrence of the different types of landslides, and
• the assignment of weights to the individual causative factors, the formulation of decision rules and the designation of susceptibility classes.

When making use of GIS techniques, the following methodological approaches can be differentiated:

• heuristic qualitative approach, particularly suited for small-scale regional surveys. The scale of such surveys is in the order of 1:100.000 to 1:250.000. They are used mostly by regional planning agencies.
• statistical quantitative approaches for medium scale surveys. These are in the range of 1:25.000-1:50.000, and are used by consulting firms or planning agencies for the preliminary planning of infrastructural works, such as the definition of road corridors. The methods at this scale can be subdifferentiated as follows:
• data driven multivariate statistical analysis
• experience driven bivariate statistical analysis
• predictive modelling through the application of probability and favourability functions
• deterministic approach for detailed studies at large scale (1:2.000 - 1:10.000), without entering at the level of the engineering geological site investigation. Such small scale studies are used by consulting firms or local planning agencies for the detailed planning of infrastructural works.

As observed before, all three methodologies require a good idea on the spatial distribution of landslides as the essential element for the analysis, although the landslide inventory mapping has to be minimized at the small scale in regional surveys to maintain an acceptable cost/benefit ratio. Therefore, the heuristic qualitative approach particularly suits reconnaissance phases, when an assessment has to be made without the time consuming inventories of landslides and all possible terrain parameters. In such cases the role of the professional expertise, leading to a classification, is essential.

A landslide inventory is executed with the objective to obtain a good insight on the whole slope instability record of the area. The inventory should give an as good as possible characterization of the landslides, such as type and subtype, as well as degree of activity or size. Historic databases are most useful for this work. However, most of the landslide distribution mapping will be obtained by aerial photo interpretation. The scale of the photos should not be smaller than 1:25.000, otherwise an important part of the slope failures will be overlooked. The use of infrared (false) colour photography is advocated, as these are more sensitive for variations in drainage and vegetational conditions, two parameters strongly related to the occurrence of landslides. To obtain a full idea on the occurrence of landslides, the study of sequential coverages is almost indispensable, as erosion and overgrowing by vegetation will wipe out the evidences for slope movements in a few years. This is particularly needed for large scale surveys, but can also be applied at medium scales. The analysis of sequential aerial photograph coverages will offer furthermore information on the degree of activity of the different types of processes, as well as the possible influence of changes of land use and other human activity on the stability of the slopes.

The image interpretation is sustained by fieldwork, normally accompanied by a systematical data collection of the terrain parameters associated with the slope failures. A detailed description for the differentiation of landslide types and degree of activity from stereoscopic photo interpretation procedures is given by Soeters and van Westen (1996).

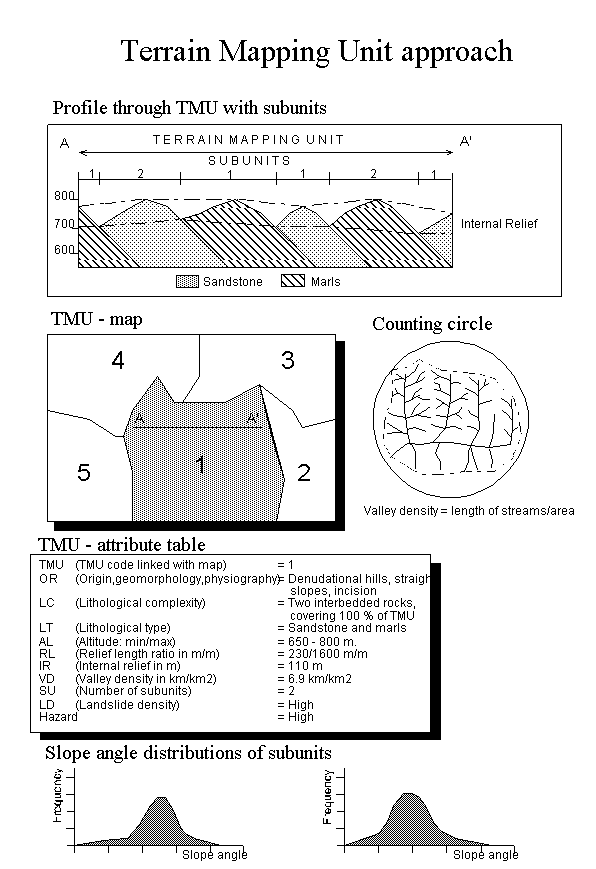
The heuristic qualitative approach is a direct or semi-direct mapping methodology, which implies that during the landslide inventory a direct relationship is made between the occurrence of slope failures and the causative terrain parameters. An a-priori knowledge on the causes of landslides is essential in the decision making and therefore the method relies heavily on the professional experience of the expert. During the photo interpretation of representative areas and in the fieldwork, the terrain conditions are evaluated at all places where landslides are encountered and preliminary conclusions are made on the causative factors. The analysis in GIS of the systematic collected data can support the expert opinion and is used to establish weight factors for the variables. Subjective, mainly on experience based, decision rules are formulated and geomorphological units are reclassified according their degree of susceptibility. For very large areas, so called Terrain Mapping Units are defined on the basis of airphoto- and satellite image interpretation. These TMUs are considered homogeneous at a scale of 1:100.000. They are subdivided into smaller units. Each units is characterized by a number of factor, such as lithology, internal relief, drainage density, which can be derived partly from overlaying the TMU map with a Digital Elevation Model in a GIS. A schematic overview of the various factors which describe a TMU is given in figure 1.

The methodology for assigning hazard classes is essentially the same as the conventional techniques used in the assessment of the stability of slopes, with the advantage that GIS offers the possibility for a weighting of parameters and an easy display of slight modifications in the decision rules and the comparison of the results with the conception of the expert. The main criticism on the methodology is the subjectivity in the decision making. However, it should be realised that subjectivity is not necessarily bad, considering that it is based on the opinion of an expert. The reproducibility of subjective classifications is normally low, which can have legal consequences, which made that practical applications were limited sofar.

In the statistical approach an indirect mapping methodology is followed. All possible causative terrain parameters are entered into a GIS and crossed for their analysis with a landslide distribution map. When using multivariate statistical methods all parameters at sites of instability can be analysed by multiple regression techniques, or parameter maps are crossed with landslide distribution maps and the correlation is established for stable and unstable areas with discriminant analysis. A schematic overview of the method is given in figure 2.

Recent examples of multivariate statistical analysis in landslide studies using GIS's have been presented mainly by Carrara (1988; Carrara et al, 1992). In his work grid cells , morphometric units, or unique condition polygons are reclassified into hazard classes according to the terrain parameters belonging to these grid cells or mapping units. The methodology is typically data driven and therefore highly objective. A difficulty in the application of multivariate statistics relies in the extremely voluminous matrices that are necessary for the calculations if reasonable small grid cells are used. On the other hand, when the grid cells are increasing in size (Carrara used cells of 100x100 m.) they become less homogeneous and consequently it is more difficult to assign a specific parameter class or the presence or absence of a landslide to a grid cell, when they affect only a small part of a it. This results in the introduction of errors in the evaluation of the relation between landslide and parameter class (See figure 3). The homogeneity of the units, to which the statistical calculations are applied increases considerably when geomorphological terrain units are used. However, the interpretation of these units at the necessary detail is a very time consuming job, asking also for a high professional knowledge. Therefore, the choice of small first order catchments and morphological terrain units is an acceptable compromise. The units can be differentiated automatically by the use of a detailed digital terrain model, and these natural units are more homogeneous than grid cells

By the use of bivariate statistical methods, the role of individual or combinations of parameters in regard to slope failures is statistically evaluated. Many statistical methods exist to determine the contribution of a certain parameter class to the occurrence of a landslide. Van Westen et al (1993) used simple density functions to determine weights for the parameter classes (See figure 4).

A differentiation can be made between the normalisation of the number of landslides occurring per parameter class and the number of pixels with landslides over the total number of pixels in a parameter class. The overall density of landslides in the area can be used as standard in the calculation of the weights, by comparing the class density with the overall density. Yin and Yan (1988) define an information value to calculate the susceptibility for the occurrence of a slide, which is logarithm of the ratio between the density of landslides in a class over the density of landslides for the whole area.

Other authors (see for example Bonham-Carter, 1994) are using the fuzzy logic or the Bayesian approach to the problem of combining datasets. Chung and Fabbri (1993) developed statistical procedures under the name of predictive modelling, applying favourability functions on individual parameters. Using these statistical and probabilistic methods, terrain units or grid cells are transformed to new values representing the degree of probability, certainty, belief or plausibility that the respective terrain units or grid cells may contain or be subject to a particular landslide.

The bivariate statistical methods give a satisfactory combination of the (subjective) professional geared direct mapping and the (objective) data driven analytical capabilities of a GIS. The main advantage of bivariate statistical procedures is, that the determination of parameters or parameter combinations used in the assessment is determined by the professional, who executes the analysis. This enables the introduction of expert opinion into the process.

Bivariate statistical methods have a serious drawback; they are using the assumption of conditional independence. This means that the different parameter maps are independent with respect to the probability for the occurrence of a landslide. This assumption is mostly not valid, however, leading to probability values which are not realistic. The problem can be avoided when the user evaluates the data and makes new parameter map by combining the dependent ones.

Both the bivariate- as well as the multivariate statistical methods in general have some other drawbacks. To test the accuracy of the prediction the final hazard map is compared with the landslides in the area, and through an iterative process of analysis and classification an optimalization of the model is established. This is however a kind of circle reasoning, which should be avoided. To avoid this use should be made of multitemporal landslide maps. The models is constructed using a landslide map of an earlier period (e.g. one decade ago), and the resulting map is checked with the present landslides.

The most serious drawback of the use of statistical methods is the collection of data over a large area regarding landslide distribution and factor maps. To effectuate this data gathering at an acceptable cost level can be a serious problem. Therefore the use of training areas and prediction (target) areas have been tested (Naranjo et al., 1994). A training area is defined as a small area within the overall study area, representative for the variability in the whole area. The occurrence of landslide in relation to the terrain conditions is analysed in detail in this sample area and the decision rules determined are extrapolated over the whole study zone, the prediction area. The results of the research show that the direct application of this methodology has serious limitations. The methodology asks for a careful confrontation of the hazard prediction with the "real world" and a adaptation of decision rules there where differences are observed, this mostly on experience driven criteria.

The advantage of the application of deterministic models in landslide hazard studies is that use is made of sound physical models. Stability models, as used in geotechnical engineering, are calculating the stability of a slope, using parameters as normal stress, angle of internal friction, pore water pressure, etc.. They result in a safety factor, which can be used directly by engineers in the design of infrastructural or remedial works. Deterministic slope stability models have been used since the beginning of this century to calculate the stability of individual slopes (Nash, 1987). Only recently several researchers have started to use the same models for the calculation of slope stability maps for larger areas such as catchments (Ward et al, 1981, Ward et al, 1982; Okimura and Kawatani, 1987; Brass et al, 1989; Benda and Zhang, 1990; Van Asch et al, 1992, 1993; Van Westen et al, 1993, , Terlien et al, 1995; Terlien, 1996) or road corridors (Hammond et al, 1992).

Hydrological models are frequently used to give an estimation of the maximum pore water pressures to be expected on the potential slip surfaces. In tectonically active regions the spatial distribution of ground accelerations as a consequence of earthquakes has to be incorporated in the final stability calculations as well (Brass et al, 1989; Van Westen et al, 1993). Several researchers also included the uncertainty in the input data in their calculations (eg. Hammond et al, 1992; Van Westen et al, 1993).

However, the use of deterministic hydrological models in combination with stability models has been successfully applied (Terlien et al., 1995; Terlien, 1996).

Due to the high spatial variability of the geotechnical parameters and the labourious methods in acquiring these data, an acceptable approximation of the values is almost only attainable at the level of site investigation, which implies a serious limitation of these models in slope stability hazard zoning at a reasonable cost/benefit ratio.

In hydrological modelling and in slope stability calculations GIS can play an important role because of its computation power, and the elaboration of Digital Terrain Models (DTMs) and derived maps such as slope maps, aspect maps and slope length maps (Wadge, 1988). These maps are required for two-dimensional (2-D) and three-dimensional (3-D) hydrological modelling and slope stability calculations.

Deterministic landslide hazard zonation can only be successful when the failure- and trigger mechanisms of different landslide types are correctly identified and modelled. In figure 5 an example is shown of such an evaluation from an area in the Colombian Central Cordillera (Terlien, 1996).

On the basis of a statistical evaluation of the relation between rainfall and landslides events, the monitoring of pore water pressure fluctuations in soils on landslide-prone slopes and the back analysis of failed slopes, a number of hydrological failure mechanisms could be recognised:

• landslides triggered directly by rainfall, caused by the saturation of the topsoil during intense rainstorms. Especially in tropical soils this mechanism is thought to be a very important landslide trigger (Anderson and Kemp, 1991);
• landslides triggered by a perched watertable in more permeable materials, which occur between more impermeable materials. Rulon and Freeze (1985) give a review of this process;
• landslides triggered by ground water. Landslides may be triggered by a combination of shear strength reduction due to saturation in the upper part of the soil profile and build up of positive pore water pressures in the lower part of the soil profile, or by convergence of saturated subsurface flow and groundwater flow in terrain concavities and hollows (eg. Okimura and Kawatani, 1987; Terlien, 1996).

Hydrological and slope stability calculations can be performed within or outside the GIS environment. If the calculations are performed outside GIS with existing hydrological and slope stability models, GIS is used as a spatial data base for storage, display and updating of the input data. Data has to be exported from the GIS to the external software and the results from the models are imported again in order to display them.

When one-dimensional models (eg. Infiltration models for vertical water flow) or two-dimensional models (eg. Hillslope hydrological models for vertical and downslope water flow) are used, the model outcome which has to be used in distributed slope stability calculations, has to be converted into a map. This is generally achieved by linking the model outcome to mapping units or slope configurations (Terlien, 1996; Van Westen et al, 1993).

One dimensional slope stability calculations can easily be performed in a raster GIS. In fact the one-dimensional infinite slope model (Graham, 1984) which calculates the stability of each individual pixel, and ignores the influence of its neighbouring pixels, is most frequently used. More complex slope stability models generally operate on cross sections. The construction of a safety factor map from a large series of cross section in GIS is rather complicated.

To overcome the problems related to the use of external models, deterministic model calculations can be performed entirely within the GIS. The disadvantage of this approach is that in most GIS packages only simple operations such as map overlaying and classification can be performed. The facilities to use complex algorithms, iteration procedures, the use of neighbourhood operations, the third dimension and the time dimension are poorly developed in most 2-D GIS packages (Coppock, 1995). A schematic overview of the use of deterministic slope stability methods in a GIS is presented in figure 6.

The final stage in deterministic landslide hazard zonation consists of the calculation of failure probability maps. To convert safety factor maps into failure probability maps use is made of the probabilities of the triggering event (time probability), as well as the variance of the input data (variable probability: the probability that the safety factor, based on the distributions of the input data will be less or equal to 1). For the latter either Monte Carlo simulations (Hammond et al, 1992) or mathematical error propagation methods (Burrough, 1986) can be used.

As a general conclusion it can be stated that hydrological models and slope stability models can be applied successfully when the triggering mechanisms are well understood and properly modelled. The poor quality of input data and the lack of verification are the principal limitations for the use of hydrological models and slope stability models in GIS-based landslide hazard zonation.

It should be understood that the results obtained with these methods cannot be used for slope stability design purposes, but they are suited for the determination of slope segments with a higher failure probability and to run scenarios when the effect of slope modifications, for example for road cuts, has to be evaluated.

GIS has proved to be an excellent tool in the spatial analysis of the terrain parameters for landslide hazard zonation. Good results are obtained in regional reconnaissance maps, when experienced based conclusions on hazard susceptibility are qualitatively extrapolated over large areas. The development of expert systems are promising for small scale landslide hazard surveys. The maximum benefit of GIS is obtained at larger scales, when the causative factors are determined by a statistical analysis of terrain parameters in relation to the occurrence of landslides. Bivariate statistical methods are preferred over multivariate statistics, as the professional can use his experience in the determination of the parameters or parameter combinations chosen for the analysis. In an iterative process the optimization of the hazard model can be achieved. The results of the application of deterministic models in GIS-based hazard zonation are positive as long as the quality of the input data is good and sufficient knowledge exists on the relation of the occurrence of the triggering mechanisms in relation to the occurrence of landslides.

Anderson, M.G. and Kemp,M.J. (1991) Towards an improved specification of slope hydrology in the analysis of slope instability problems in the tropics. Progress in Physical Geography, Vol. 15, No. 1: 29-52.

Asch , Th. W. J. van, Westen, C.J. van, Blijenberg, H. And Terlien, M.T.J. (1992) Quantitative landslide hazard analysis in volcanic ashes of the Chinchina area, Colombia. Proceedings Primer Simposio Internacional sobre sensores remotos y sistemas de informacion geografica pare el estudio de riesgos naturales, Bogota, Colombia: 433-443.

Asch, Th. W. J. van, Kuipers, B. And Zanden, D.J. van der (1993) An information system for large scale quantitative hazard analysis on landslides. Zeitschrift fur Geomorphologie N.F., Suppl.-Bd 87: 133-140

Bonham-Carter, G.F.(1994) Geographic Information Systems for Geoscientists; modelling with GIS. Computer methods in Geosciences, Vol. 13, Pergamon Press, pp. 398

Benda, L. and Zhang, W. (1990) Accounting for the stochastic occurrences of landslides when predicting sediment yields. Proceedings of the Fiji Symposium, IAHS-AISH Publ. 192: 115-127

Brass, A., Wadge, G. And Reading, A.J. (1989) Designing a Geographical Information System for the prediction of landsliding potential in the West Indies. Proceedings Economic Geology and Geotechnics of Active Tectonic Regions, London, England.

Burrough, P.A. (1986) Principles of Geographic Information Systems for land resource management. Monographs on Soils and Resources Surveys, No. 12, Clarendon Press Oxford, 193 pp.

Carrara, A. (1988) Multivariate models for landslide hazard evaluation. A "black box" approach. Workshop on Natural Disasters in European Mediterranean Countries, Perugia, Italy, pp 205-224.

Carrara, A., Cardinali, M. And Guzzetti, F. (1992) Uncertainty in assessing landslide hazard risk. ITC Journal 1992-2: 172-183

Chung, C.F. and Fabbri, A.G. (1993)The representation of geoscience information for data integration. Nonrenewable Resources, Vol. 2:2, pp.122-139

Coppock, J.T. (1995) GIS and natural hazard: an overview from a GIS perspective. In: A. Carrara and F. Guzzetti (eds) Geographic Information Systems in Assessing Natural Hazards, Kluwer Academic Publishers: 21-34

Fournier d'Albe, E.M. (1976) Natural Disasters. Bull. Int. Assoc. of Eng. Geol., Vol.14, pp. 187

Graham,J. (1984) Methods of slope stability analysis. In: D. Brunsden and D.B. Prior (eds), Slope Instability, John Wiley & Sons: 171-215

Hammond, C.J., Prellwitz, R.W., and Miller, S.M. (1992) Landslide hazard assessment using Monte Carlo Simulation. In: D.H. Bell (ed), Proceedings of the sixth International Symposium on Landslides, Christchurch, New Zealand, Balkema: 959-964

Naranjo, J.L., van Westen, C.J., and Soeters, R. (1994) Evaluating the use of training areas in bivariate statistical landslide hazard analysis- a case study in Colombia. ITC Journal 1994-3: 292-300

Nash, D. (1987) A comparitive review of limit equilibrium methods of slope stability analysis. In: M.G. Anderson and K.J. Richards (eds) Slope stability. John Wiley& Sons: 11-75

Okimura, T. and Kawatani, T. (1987) Mapping of the potential surface failure sites on granite mountain slopes. In: V. Gardiner (ed). International Geomorphology, Part 1, John Wiley & Sons: 121-138

Rulon, J.J. and Freeze, R.A. (1985) Multiple seepage faces on layered slopes and their implication for slope stability analysis. Canadian geotechnical journal, Vol. 22: 347-356.

Swiss Reinsurance Company (1990) Economic losses and insured losses due to natural disasters 1960-1989, Sigma 2/90

Terlien, M.T.J., Asch,Th.W.J.van and Westen, C.J. van (1995) Deterministic modelling in GIS-based landslide hazard assessment. In: Carrara, A. and Guzzetti, F. (Eds.) Geographical Information Systems in assessing natural hazards, Kluwer Academic Publishers: 57-77

Terlien, M.T.J.(1996) Modelling spatial and temporal variations in rainfall-triggered landslides. PhD thesis, ITC Publ. Nr. 32, Enschede, The Netherlands, 254 pp.

Varnes, D.J.(1984) Landslide Hazard Zonation: a review of principles and practice. Commission on landslides of the IAEG, UNESCO, Natural Hazards No. 3, 61 pp.

Wadge, G. (1988) The potential of GIS modelling of gravity flows and slope instabilities. Int. J. Geographic Information Systems, Vol. 2, No. 2: 143-152

Ward, T.J., Li, R.M. and Simons, D.B. (1981) Use of a mathematical model for estimating potential landslide sites in steep forested drainage basins. In: Erosion and sedimentation in the Pacific Rim steeplands, IAHS publ. 132: 21-41

Ward, T.J., Li, R.M. and Simons, D.B. (1982) Mapping landslides in forested watersheds. Journal of the geotechnical engineering division, Vol. 8: 319-324

Van Westen, C.J., Van Duren, I, Kruse, H.M.G., and Terlien, M.T.J. (1993) GISSIZ: training package for Geographic Information Systems in Slope Instability Zonation. ITC-Publication Number 15, ITC, Enschede, The Netherlands.Volume 1: Theory, 245 pp. Volume 2: Exercises, 359 pp. 10 diskettes