DETERMINISTIC MODELLING IN GIS-BASED
LANDSLIDE HAZARD ASSESSMENT
M.T.J. Terlien, C.J. van Westen
International Institute for Aerospace Survey and Earth Sciences (ITC)
P.O. Box 6, 7500 AA Enschede, the Netherlands
Th.W.J. Van Asch
University of Utrecht
Heidelberglaan 2, 3584 CS Utrecht, the Netherlands.
(Terlien, M.T.J., Asch,Th.W.J.van and Westen, C.J. van (1995
) Deterministic modelling in GIS-based landslide hazard assessment. In: Carrara, A. and Guzzetti, F. (Eds.) Geographical Information Systems in assessing natural hazards, Kluwer Academic Publishers: 57-77)![]()
ABSTRACT
Deterministic models are based on physical laws of conservation of mass, energy or momentum. In the case of deterministic landslide hazard zonation, distributed hydrological and slope stability programs are used to calculate the spatial distribution of groundwater levels, pore pressures and safety factors. This paper is concentrated on the integration of two-dimensional, raster-based, geographic information systems (GIS) and deterministic models, with emphasis on deterministic hydrological models. Three examples of deterministic landslide hazard zonation are presented; one from Costa Rica and two from Colombia. In the example from Costa Rica, a one- dimensional external hydrological model is used to calculate the height of perched water tables in the upper metre of the soil for different soil types and different rainstorms. In the first example from Colombia, an external two-dimensional hydrological model is used to calculate the maximum groundwater level, for a 20 year period, in different slopes with a sequence of volcanic ashes overlying impermeable residual soils. In the second example from Colombia, a three-dimensional hydrologic model is used in a GIS to simulate groundwater fluctuations during one rainy season. In examples 1 and 2 the results of the hydrologic calculations are used in stability calculations to obtain maps which give the spatial distribution of safety factors and the probability of failure, with the use of distribution functions of the input parameters. In example 3 the calculated groundwater levels are exported to an external slope stability model to calculate the safety factor along slope profiles.
![]()
1. Introduction
Deterministic, or physically-based, models are based on physical laws of conservation of mass, energy or momentum. The parameters used in these models can be determined in the field or in the laboratory. Most deterministic models are site-specific and do not take into account the spatial distribution of the input parameters. Models which take into account the spatial distribution of input parameters are called distributed models. Deterministic distributed models require maps which give the spatial distribution of the input data. GIS is a tool for collecting, storing, retrieving, transforming, manipulation and displaying spatially distributed data and therefore it is frequently used in distributed deterministic modelling (De Roo, 1993).
In deterministic distributed modelling the spatial distribution of the input parameters should be assessed by interpretation of aerial photos and satellite images, fieldwork, and laboratory analysis. The following step is entering the data in a GIS. The most frequently used method is digitizing the data and converting it to a raster format. Because of its simple data structure and easy integration with remote sensing data, the raster format is widely used in spatial analysis, simulation and modelling. In a raster-based GIS, an area is subdivided in cells or pixels. Each cell or pixel can be treated as a homogeneous area with one or more attribute values. The spatial distribution of the input parameters is represented as maps which give for each pixel the value of the parameters necessary in the deterministic calculations, such as soil strength, soil density, soil depth, depth of the groundwater table, surface topography and seismic acceleration.
The deterministic calculations can be performed within or outside the GIS. If the calculations are performed outside the GIS, the system is only used as a spatial database for storing, displaying and updating the input data. The main advantage of this approach is that external existing models can be used without losing time in programming the model algorithms into the GIS. A disadvantage of model calculations outside the GIS is data conversion to and from external models. Data conversion can be a major problem because most programs have their own data format and data structure. Some even have special input modules which only allow manual data entry. Only when the programs require input data in ASCII format, can conversion be relatively easy. Another disadvantage of using external models is the representation of the results of the model calculations, which are normally not spatially distributed, in the form of maps in a GIS. Interpolation of model results, which are normally in points or along profiles, is a major problem.
![]()
2. Deterministic landslide hazard zonation and GIS
In the case of deterministic landslide hazard zonation, distributed hydrological and slope stability models are used to calculate the spatial distribution of piezometric levels, pore pressures and safety factors. Most of the hydrological models which have been developed for the calculation of piezometer levels and pore pressures are either one-dimensional (e.g. infiltration models for vertical water flow) or two-dimensional (e.g. hillslope hydrologic models for vertical and downslope water flow). Because the results of these model calculations have to be used in subsequent GIS operations (e.g. stability calculations) they have to be converted to a map. Three- dimensional hydrologic models have the problem of converting the output map to a format which can be entered in the GIS for further calculations. Slope stability models calculate the safety factor for a slope in two or three dimensions. Since an area consists of many slopes, the use of these models to obtain the spatial distribution of safety factors is very time consuming as every slope should be analyzed separately. To overcome the problem of data conversion, deterministic model calculations can be performed within the GIS. The disadvantage of this approach is, however, that only simple models can be applied due to limitations with respect to the use of complex algorithms, iteration procedures and the third dimension in the conventional, two-dimensional GIS. Currently, only infinite slope models, which allow for the calculation of the safety factor for each pixel individually, are applied inside such GIS systems. Only, when more sophisticated, three-dimensional GIS systems are used, this problem can be solved satisfactory.
The choice of using external or internal hydrologic models in relation to a GIS also depends on the landslide type. Landslides which are triggered by infiltrating rain and perched water tables require a hydrological model which emphasizes the vertical saturated and unsaturated flow (Van Asch, 1992). These models are mathematically complex due to the relation between soil moisture and hydraulic conductivity. This, in combination with the fact that complex modelling in a vertical direction is quite difficult in a two-dimensional GIS, hinders the use of these models in conventional GIS systems. Currently they are mostly used outside the GIS. The results of these models have to be linked to terrain characteristics or soil types to obtain a map with pore pressures which can be used in stability calculations. Landslides which are triggered by groundwater levels on the contact of two soils with varying permeability, can be predicted with a 3-dimensional groundwater model. As the vertical percolation is of minor importance in these situations it is modelled in a conceptual way assuming a percolation time which is estimated based on field observations. The groundwater flow in the x and y directions can be modelled with finite difference methods in the GIS if it is provided with neighbourhood functions (Okimura and Kawatani, 1987).
The stability of a slope can be calculated in 1, 2 or 3 dimensions. In one-dimensional models only the conditions of individual points in the terrain are evaluated, without taking into consideration the resulting forces of neighbouring areas. The infinite slope model, which is calculated for individual pixels, is essentially a one-dimensional model, and can be performed easily in GIS. It can give reliable results in the case of superficial landslides with a depth-length ratios smaller than 0.1. For the prediction of landslides with depth-length ratios larger than 0.1, the infinite slope model underestimates the safety factor (Van Asch et al., 1992). The underestimation increases as the depth-length ratio increases. For an accurate stability calculation, 2 or 3 dimensional models should be used. Two dimensional slope stability analysis is performed along profiles, and the resulting forces of individual slices of the profile are taken into account. In three dimensional slope stability programs, the stability of the entire landslide body is calculated. The use of 2 or 3 dimensional slope stability models in combination with a 2 dimensional raster-based GIS currently requires transfer of slope data and hydrologic data from a GIS to external slope stability programs. In many deterministic landslide hazard zonation projects, however, the infinite slope model is also used to predict the occurrence of deep landslides. In these cases the large uncertainty in the input parameters, such as piezometric levels or depth of failure surface, will not give more reliable results than with 2- or 3-dimensional models.
Three examples of deterministic landslide hazard zonation are presented in the following sections; one from Costa Rica and two from Colombia. In the first two examples, the results of the hydrologic calculations are used in an infinite slope model to obtain maps which give the spatial distribution of the safety factor and the probability of failure by using distribution functions of the input parameters. In the third example, the calculated groundwater levels are exported to an external two-dimensional slope stability model.
![]()
3. Slope stability calculations in Puriscal (Costa Rica)
In the area of Santiago de Puriscal (Costa Rica), shallow soilslips (1 to 1.5 m) occur frequently on slopes steeper than 30 degrees, covered with residual soil from volcanic Tertiary rocks, and varying in depth from 0.5 to 5 m. The most important land use is pasture for cattle breeding as well as corn, tobacco, sugar cane and bananas.
A pilot area of approximately 3 km2 was selected (see figure 1) to model in a deterministic way, supported by the GIS, the temporal and spatial frequency of soilslips and to analyze the influence of land use. Hydrological monitoring and back analyses of investigated soil slips in the field revealed that no permanent groundwater tables occur in the upper part of the soils on the steep slopes and that failure can take place without the occurrence of high pore water pressures. The soils remain unsaturated most of the time and have a relatively high cohesion, due to soil moisture suction. Failure occurs due to local water concentration at critical depths where the soils become nearly saturated or show slightly positive pore pressures. Under these conditions the soil strength has reached its minimum value. For the modelling of the soilslip frequency, strength characteristics of the soil are needed which describe the relation between cohesion and the amount of soil water suction.
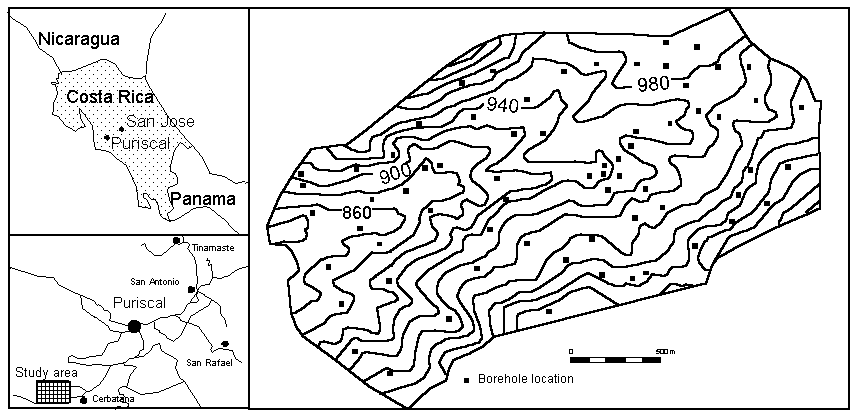
Figure 1: Location of the study area near Puriscal (Costa Rica). The detailed map shows the borehole locations.
The hydrological triggering system for these soilslips can be analyzed by a 1- dimensional soil-water balance model, which describes in detail the unsaturated water fluxes in the upper 2 metres of the soil. These are controlled by processes like interception, infiltration, unsaturated throughflow and water root uptake by vegetation (evapotranspiration). Important hydrological parameters, controlling these processes, are related to the soil texture of the different layers in the profile. Soil moisture monitoring carried out in this area showed no net change in soil moisture storage per day in the rainy season with regular daily showers. Positive daily storages were observed in case of extreme precipitation. Important soil moisture fluctuations occur within one day and show a maximum in the root zone (till 150 cm) while at a depth of 150 to 200 cm the soil moisture content remains mainly constant.
Figure 2 gives the flowchart of the operations carried out inside and outside the GIS for the spatial and temporal modelling of soilslip frequency in the Puriscal area. The first step was the modelling of the soil moisture distribution for different types of extreme rainstorms and different types of soil profiles. Therefore a soil survey was carried out in a sample area of 3 km2 to map the distribution of the upper 2 metres of soil profile types. Seven soil profile types were distinguished in the area on the basis of thickness and texture of the different layers (figure 3). In general, a silty clay A-horizon was found on top of a more clayey layer, which changes at greater depths into more sandy or granular material or weathered rock. The seven soil profile types were used for the hydrological modelling. Four storms were selected with a maximum intensity of 30-35 mm per hour (= the minimum infiltration capacity of the soil) and with different duration ranging from 2 to 5 hours, with return periods of 2 to 200 years.
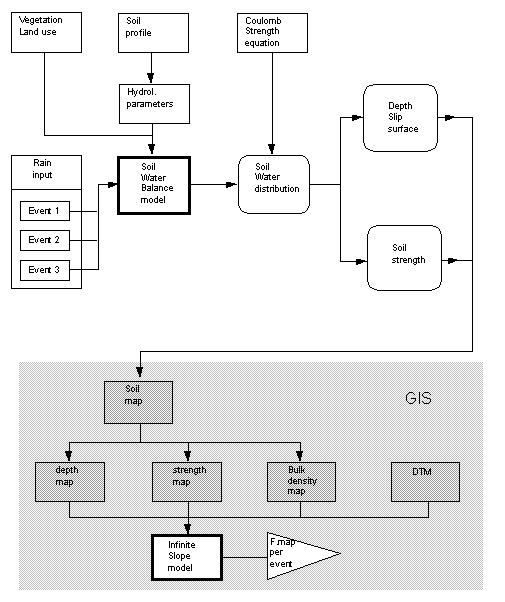
Figure 2: Flowchart of the operations carried out outside and inside GIS for the spatial and temporal modelling of soilslip frequency in Puriscal (Costa Rica)
A storm with a low intensity of 2.7 mm per hour was also selected with an extreme duration of 24 hours and with a return period of 2 years. Not only extreme rainfall events must be considered for the triggering of soilslips, but also the preceding dry period. The amount of evapotranspiration during the preceding dry period determines the initial soil moisture content at the beginning of the storm. This proved to be a very sensitive parameter in the hydrologic model. With the assumption that the extreme events take place in the wet season, the average wet initial moisture content was taken as input at the beginning of the modelling. This is a reasonable assumption because a saturated soil returns to the average wet initial soil moisture content very quickly, usually in one day.
Soil texture is the most important parameter because it is strongly related to the hydrological parameters which are needed in the hydrological model. The hydrological parameters for each soil texture were determined in the laboratory. Three important functions could be described with these parameters:
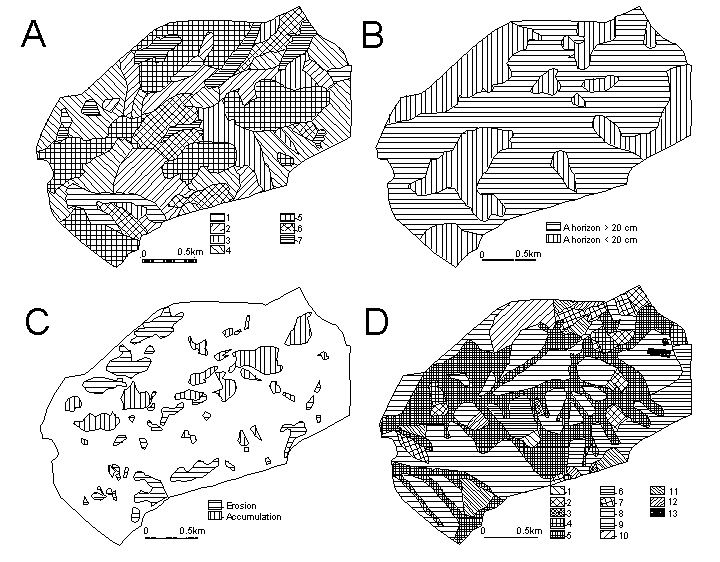
Figure 3: Some input maps of the Puriscal area. A: Soil types (1 = rock within 20 cm., 2= rock between 0.2 - 1 m, 3 = rock between 1 - 2 m, 4= clay, 5= clay on loamy clay within 1 m, 6 = clay on loamy clay between 1 and 2 m, 7 = loamy clay on sandy clay), B: Depth of A-horizont, C: Denudational processes, D: Land use (1= bananas, 2= Coffee, 3= mix coffee/trees, 4= complex forest, 5= forest, 6= high grassland, 7= maiz, 8= pasture, 9= mix of pasture and trees, 10= shrubs, 11= sugarcane, 12= tobacco, 13= houses)
The output of the hydrological modelling resulted in a distribution of the moisture content versus depth for the seven soil types and for the different rain events. The depths with the maximum soil moisture content indicate the location of the potential slip surface. In this way for each profile and each event the depth of the minimum strength in the soil could be detected which is the depth of the potential slip plane (see figure 2). The calculated depths correspond reasonably well with the observed thicknesses of translational landslides within the area.
It appeared that for 5 profile types the slip surface will develop nearly at the same depth for the different events. This is due to the fact that at this depth there is sharp difference in hydrological conductivity between two layers. Concentration of water will always occur at this boundary for all events and hence the slip surface will always develop at the boundary between these layers where concentration of water may occur. Two profile types which do not have textural boundaries show larger variation of the potential slip surface depth for different events and their depth will also vary for different slope angle classes. The flatter the slope the deeper the slip plane. Therefore it is wise to take the worst case, which is the boundary with the unweathered rock (more resistant). Hydrological model simulations were also performed for different vegetation (pastures) and crop covers (coffee, corn, sugar cane and tobacco). It appeared that for the selected types of storm events, only slight differences in moisture content for the different land cover types were observed at the critical depth where the slip surface could be expected. Therefore the effect of land use was not considered further.
Having assessed the depth of the potential slip surface and the moisture content per rain storm for each profile type, soil strength maps per event and soil depth maps could be created in GIS (see figure 2). The soil strength for different moisture contents and soil textures was determined by direct shear tests in the laboratory. Together with the digital terrain model (DTM), safety factors for each pixel were calculated with the infinite slope model (see equation 1) and safety factor distribution maps could be produced for each event with a certain return period. Table 1 gives an overview of the percentage of area which can be affected by landslides for different rainfall events. The distribution of unstable areas is strongly related to slope angle. Unstable areas are found on slopes steeper than 30 degrees. On these slopes instability is strongly related to the depth of the regolith.
As can be observed from table 1, there seems to be a maximum for the area that fails, as calculated by the model. Large durations and intensities of rainstorms do not result in large percentages of instable area, as this area is limited by other factors, such as slope angle, and depth of the soilcover.
Table 1: Percentage area affected by landslides for different rainfall events, within the Puriscal study area.
|
Event |
Intensity [mm.h-1] |
Duration [h] |
Return period |
% area failed |
|
A |
2.7 |
24 |
2 |
0.8 |
|
B |
30.3 |
2 |
4 |
0.7 |
|
C |
39.8 |
1.5 |
2 |
0.5 |
|
D |
20 |
50 |
50 |
2.8 |
|
E |
30 |
100 |
100 |
2.9 |
|
F |
35 |
200 |
200 |
3.0 |
![]()
4. Slope stability calculations in Manizales (Colombia)
The city of Manizales (300,000 inhabitants) is located at an altitude of 2000 m on the steep slopes of the western flank of the Cordillera Central, near the Nevado del Ruiz volcano (see figure 4).
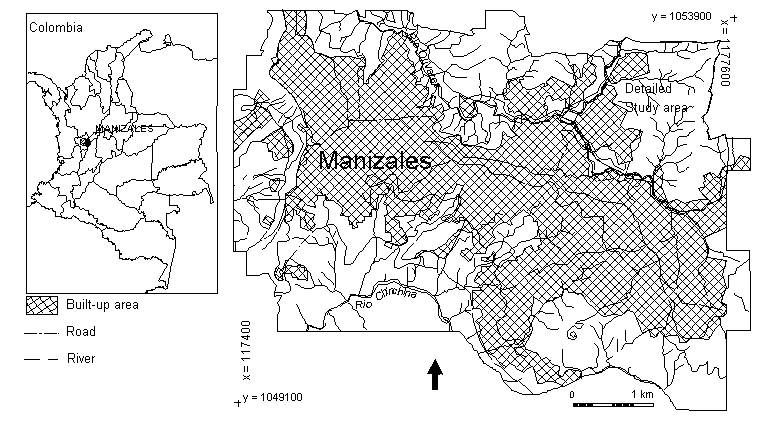
Figure 4: Location of the study areas in Manizales (Colombia). The total area displayed was used in the 1:10.000 scale study. The area in the NE corner was used for the 1:2.000 scale study.
Due to its unfavourable topographic location, large parts of the city are built on steep slopes, which are mostly modified by cuts and (hydraulic) fills to provide adequate terrain for housing. Manizales has suffered severely from landslide problems. The landslides are a result of the geological and geomorphological setting of the area, the wet climate, and the fact that the area is located in a seismically active region. An overview of landslide causes and frequencies is given by Van Westen et al. (1993). A small section of the landslide distribution and activity maps are shown in Plate 1.
The geology of the area consists of metasedimentary schists from the Quebradagrande formation of Cretaceous age covered by volcanic ashes of Quaternary age (Naranjo and Rios, 1989). The thickness of the ashes varies from 15 metres on the flat hilltops to 1 metre or less on very steep slopes. The ash deposits contain layers with textures ranging from very fine (< 63mm) to very coarse (> 5000 mm) (Mool, 1992; Van Westen et al., 1993). These changes in texture cause perched watertables in the ashes, which can trigger soilslips, soil avalanches, and translational slides. Deep-seated slides and flowslides, occurring in the area, are caused by high groundwater levels in the volcanic ashes overlying impermeable residual soil from schists of the Quebradagrande formation.
To evaluate the stability of the entire city of Manizales, comprising 33 km2, the following steps were taken:
1. Construction of an engineering geological data base;
2. Groundwater modelling;
3. Calculation of maximum horizontal seismic accelerations;
4. Slope stability calculations using different scenarios for groundwater levels and seismic accelerations; and
5. Calculations of maximum failure probability within a 20 year period.
The data set was digitized mainly from 1:10,000 scale maps, and raster maps were made with a pixel size of 8.5 m. Due to the very heterogeneous nature of the superficial materials in Manizales, its rugged topography and the small amount of drillhole information, the engineering geological database could not be obtained from interpolation of material depths derived from drillholes and outcrops. Therefore, another method was developed based on the use of logic reasoning in the GIS. With this method, the spatial distribution of the various materials could be deduced from a very detailed geomorphological map, three landslide distribution maps from different periods, a geological map, and two DTM's from different dates with accompanying slope maps. Combining the different maps using conditional statements in the GIS made it possible to produce the engineering geological database. This database describes the materials in three dimensions, showing both the spatial distribution of 4 basic material layers and their thicknesses. As we are working with a 2-dimensional GIS system, this was done by separating the spatial information from the thickness information (see figure 5). This way 8 different maps were used which provide the profile for any pixel if they are read simultaneously using a pixel-information program. The maps show the spatial distribution of the four layers with the same material codes and can be linked with tables containing geotechnical properties derived from laboratory tests.
A simple 2-dimensional model was used for the groundwater modelling (Van Asch et al, 1992). This computer model calculates ground water levels on a daily basis in layers with different hydrological properties. As we were interested in the contact between pyroclastic materials and residual soils, we used a two-layer model, under a large number of different profiles with respect to slope angle, slope length thickness of materials and saturated conductivities. The maximum groundwater levels for each of these profiles were calculated for a 20-year period and used in the construction of magnitude-frequency curves. Then the profiles were linked to the maps using the engineering geological database and the topographic information, and groundwater maps were derived for different return periods (Van Westen et al, 1993).
The effect of earthquake acceleration on the slope stability was taken into account, using the conventional, pseudo-static method of limiting equilibrium. The use of more complex dynamic models, which use strong motion earthquake records in the calculation of landslide displacement, as introduced by Newmark (1965) was not applied because of the lack of adequate data and because of the limitations of the PC-based raster GIS that we used.

Figure 5: Simplified structure of the engineering geological data base for Manizales. Separate maps are made for the spatial distribution of different layers of materials (Sequence), and for the thickness of the layers. Vertical profiles can be obtained by reading all maps simultaneously in a GIS, and combining them with geotechnical properties from tables.
For the calculation of seismic accelerations, information was obtained from magnitude-frequency curves, regional attenuation curves, the engineering geological database and groundwater maps. Amplification at the contact of different materials was calculated by comparing the densities and seismic velocities of the various layers within the engineering geological data base. Summation of these amplifications and multiplication with the peak acceleration at the rock-soil contact allowed for the calculation of horizontal accelerations at the surface for each pixel in relation to the return period of earthquakes.
A number of scenarios to calculate average safety factors were developed by combining the effects of groundwater and seismic acceleration with different return periods.
An infinite slope model (see equation 1) was used in which the average values for c' and j' were used.
![]()
Where:
F = safety factor,
c´ = effective cohesion (KPa),
g
= unit weight of soil (KN/m3),g
w = unit weight of water (KN/m3),z = depth of failure surface below the terrain surface (m),
zw = height of water table above failure surface (m),
b
= terrain surface inclination (°),j
´ = effective angle of shearing resistance (°).r
= bulk density in (kg/m3),a = horizontal component of earthquake acceleration (m/s2).
An example of a classified safety factor map, together with landslide occurrence and activity maps, for a part of Manizales, is shown in Plate 1.

Plate 1: An example of a classified safety factor map (below), together with landslide occurrence (above) and activity maps (middle), for a part of Manizales.
Use was made of error propagation techniques to calculate the distribution of F-values for each pixel, based on the distribution of the input parameters (Van Westen et al, 1993). If it is assumed that the safety factors have a normal distribution, the deviation from the F=1 value can be calculated. This deviation from the F=1 value, expressed in units of standard deviation, is called the Z-value (Blalock, 1979). The area under the curve of normalized F-values represents a probability of 1 (see figure 6). The area left of the F=1 line represents the probability that the safety factor, for a given scenario, will be less than 1. Two situations are possible:
The values for the failure probability calculated so far are only based upon the variance of the input parameters, cohesion, friction angle and soil thickness, given a certain magnitude for rainfall related groundwater and/or seismic acceleration. To derive at real probabilities, these values were multiplied with the probability that a given event, described in each of the scenarios, will occur within a given time period. In this case a design period of 20 years was used; the assumed design period for the low-budget housing projects in the Manizales area. The multiplication with the time probability will result in very low values for scenarios with high magnitudes of both groundwater levels and seismic accelerations, as the probability that both occur on the same day, is low.
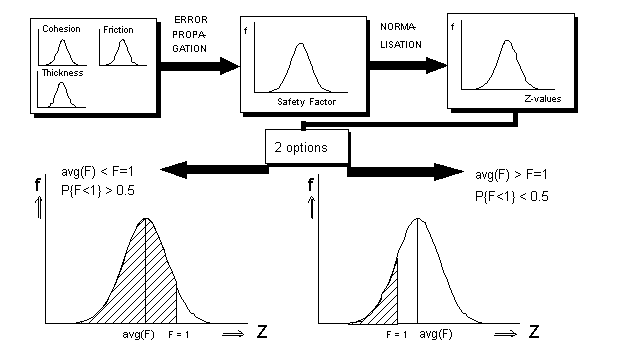
Figure 6: Simplified procedure for calculation failure probabilities. The curves show the frequency distribution of safety factors for a given pixel. See text for explanation.
For the calculation of the overall hazard map for Manizales, all possible scenarios with respect to the magnitudes of the triggering factors should be calculated, and the results represented as probability values within a 20 year design period. Fortunately, a number of scenarios with combined rainfall and earthquake effects, can be neglected, as their time-probability will be so low that it will not be significant. Therefore, a selection was made of 15 scenarios, with the effect of one single triggering factor only. Out of the 15 maps produced for each of these scenarios, the highest probability value was selected for each pixel.
![]()
5. Detailed slope stability calculations for Manizales
Two major problems were encountered in the small scale landslide hazard analysis: assessment of the distribution of the pyroclastic materials and modelling of the groundwater levels. To overcome these problems, a detailed analysis was done on a small (2.5 km2) study area in the NE sector of Manizales (see figure 4). The input data was digitized from 1:2,000 scale maps and converted to raster maps with a pixel size of 5 m. To predict the location and moment of initiation of landslides, a distributed, 3-dimensional, two-layer, groundwater model was developed in the GIS environment. It works on a daily basis and can be used for the calculation of groundwater levels in the first layer. The second layer is a semi-permeable layer of infinite thickness. In the case described in this paper, the first layer is a combination of ashes and residual soil. The second layer are schists belonging to the Quebradagrande formation. Data are extracted from the DTM, the engineering geological map which gives the spatial variability of the materials, and the groundwater map, which are used to assess profile based stability using a slope stability program outside the GIS.
The hydrologic model has four calculation procedures:
Because the amount of overland flow was very small (1-3% of the rainfall) it was neglected in the model calculations. For the calculation procedures parameter maps and input maps are required. Parameter maps are maps containing the spatial variability of time-independent variables (distribution and thickness of layers, landuse and DTM). Input maps are maps containing the spatial variability of time-dependent variables (rainfall, groundwater levels).
The following three parameter maps are required:
The following two input maps are required:
For every time step an output map with the new groundwater level is calculated. The flowchart of the model with the calculation procedures, the parameter maps, the input maps and the output map is given in figure 7.
The net rainfall is the rainfall which enters the soil. When overland flow is neglected the net rainfall can be calculated by subtracting the interception loss from the initial rainfall. From existing studies (Rijtema, 1965; Aldridge and Jackson, 1968) two general logarithmic relations have been derived to calculate the interception for grass and for trees. The constants in these relationships are attribute values of the landuse map. If the amount of rainfall and the type of vegetation is known the net rainfall can be calculated.
The evapotranspiration can be calculated with the Penman method (Doorenbos and Pruitt, 1984) or with the Thornthwaite method (Thornthwaite and Mather, 1957). In this research the evapotranspiration is estimated based on existing data. These data indicated that 55% of the precipitation will be lost by evapotranspiration. Therefore, from every rainstorm only 45% will percolate through the root zone. For small rainstorms this will be an underestimation of the evapotranspiration and for large rainstorms it will be an overestimation.
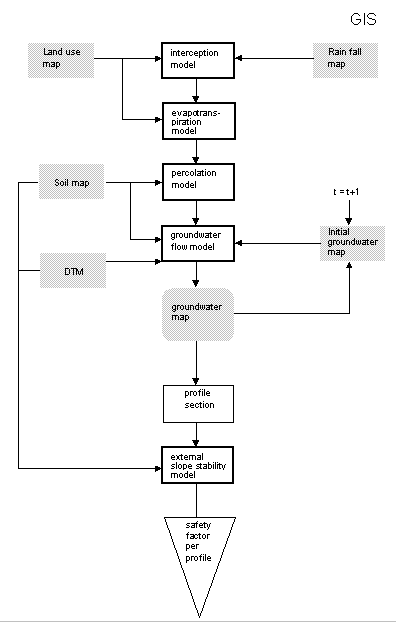
Figure 7: Flowchart of the operations carried out for the detailed slope stability in Manizales (Colombia).
The vertical percolation is not modelled in a deterministic way because of the limitations of the GIS system which was used (ILWIS) and because an estimation of the percolation rate is enough for an acceptable prediction of groundwater levels. Based on field observation a vertical percolation of 2.5 m.day-1 was used.
The vertical percolation in this model is independent of the initial moisture content of the soil and the soil moisture distribution.
The downslope flow of water in the unsaturated zone is not modelled. Runs with a 2-dimensional hydrologic models indicated that the percentage of rainfall lost by downslope unsaturated flow increases as the depth of the groundwater level increases. In this model this percentage is independent of the depth of the groundwater level and is estimated at 20% of the rainfall.
The groundwater flow on the contact between the first and second layer is modelled using a finite difference approach (Okimura and Kawatani, 1987). The new groundwater level in a cell can be calculated with the following two formulas:
![]()
![]()
Where:
Hnew = New height of saturated zone [cm]
Hold = Old height of saturated zone [cm]
H = Height of saturated zone [cm]
T = Time [day]
P = Precipitation [cm.day-1]
I = Interception [cm.day-1]
E = Evapotranspiration [cm.day-1]
Ksat1 = Saturated hydraulic conductivity layer 1 [cm.day-1]
Ksat2 = Saturated hydraulic conductivity layer 2 [cm.day-1]
pv = Pore volume between pF=0 and pF=2.2 [dimensionless]
a
= Slope angle of the terrain [degrees]Field observations indicated that the existing topography resembles the bedrock topography and therefore the DTM is used for the calculation of the slope angle of the bedrock in x- and y-directions. Equation 3 has to be solved iteratively because sometimes the sum of the outgoing fluxes exceeds the total amount of water in a cell.
The quantification of the model parameters in order to obtain a close fit between the model result and reality is known as model calibration (Kirkby et al, 1987). The saturated conductivity of the first layer (ashes and residual soil) is determined by field measurements. The saturated conductivity of the bedrock could not be measured in the field and is assessed by optimization. The value for this parameter was adjusted several times so that the best fit was obtained between the calculated values and the measured values in the field.
A storage capacity of 0.2 was used in the final model calculations because no satisfactory fit could be achieved with the laboratory values of this parameter (0.1). The assumptions on the vertical percolation rate in the unsaturated zone are probably the reason that this higher value resulted in a better fit. As the objective of the model is the exact prediction of the groundwater level at every pixel, but to give an indication of the distribution of the groundwater level in the ashes, no submodels were incorporated for a better estimation of the unsaturated flow. The values for the most important parameters which were used in the model calculations are given in table 2. Some examples of groundwater maps for a part of the study area are given in figure 8.
Table 2: Values for parameters used in groundwater simulations
|
Percentage rain reaching groundwater |
25% |
|
Storage capacity |
0.2 |
|
Ksat layer 1 [cm.day-1] |
10.0 |
|
Ksat layer 2 [cm.day-1] |
0.55 |
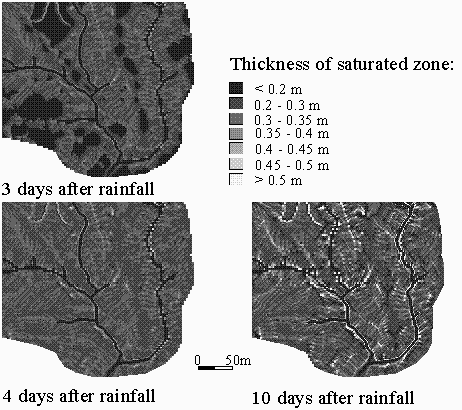
Figure 8: Some examples of the groundwater model output for a part of the study area. Three maps show the thickness of the saturated zone on the contact of the volcanic ashes with the underlying residual soils, for 3, 4 and 10 days after a major rainstorm.
The calculated groundwater maps and the ash thickness map can be used for stability calculations of slopes which show signs of instability in the field. The topographic profiles of these slopes are crossed with the engineering geological map and the groundwater map and converted to a file which can be used in the computer program SLIDE (Van Asch, 1992) for stability calculations (see figure 6).
The program SLIDE offers the possibility to specify the depth of the failure surface in a file or to analyze the profile in order to find the failure surface with the lowest safety factor. In this example the groundwater map of day 32 was selected because the highest groundwater levels were calculated for this day. For day 32 the safety factor was calculated for a convex ash covered slope north of Manizales. In the first calculations with SLIDE the contact between residual soil and weathered schists was selected as the failure surface. The minimum safety factor in this case was 2.18 which indicated that the possibility for a landslide with its failure surface in the residual soil is very low. Since the residual soil is not the only layer in which failure surfaces can develop, SLIDE was used to find the location of the failure surface with the lowest safety factor. The lowest safety factor on the slope was 0.94 for a failure surface in the ashes. Because the failure surface of such a landslide is above the highest simulated groundwater levels it is probably caused by perched watertables in the ashes and not by groundwater levels on top of the schists. The advantage of the use of SLIDE in this case is that various types of failure surfaces can be analyzed while in the GIS only infinite slope stability calculations can be performed.
![]()
6. DISCUSSION AND CONCLUSION
The use of deterministic models in landslide hazard analyses has not the pretention to calculate in an absolute and precise way the safety factor at each site in the terrain. This is not realistic because the amount of data necessary to assess the spatial distribution of parameters needs a tremendous amount of effort (Mulder, 1991). However hazard zonation in a quantitative way can be done using a probabilistic approach: the probability of failure can be assessed in landslide prone areas by using distribution functions of parameters (Van Asch and Mulder, 1988; Van Asch and Sukmantalya, 1993; Ward et al, 1982). A stochastic approach can be used for temporal modelling of landslide frequency for specific landslide prone sites showing one type of landslide. The selection of these sites can be done in a GIS database for landslide hazard zonation (Van Asch and Sukmantalya, 1993; Van Asch et al, 1992). A successful simulation can be performed if within these landslide prone sites enough data are available to determine the variation in the hydrological and geotechnical parameters. The use of stability models in a probabilistic way may have the advantage, as compared to other models, that the necessary hazard parameters are weighed in an exact way based on physical models, calculating stability. Also the use of statistical analyses enables one to obtain a weighing of relevant factors in the form of empirical equations, but these equations are based on the presence or absence of landslides and it is therefore doubtful whether they give reliable hazard scores in areas without landslides but with necessary failure conditions (Van Asch and Mulder, 1991). A combination of statistical and deterministic analyses in certain key areas can test the reliability of empirical statistical equations in potential dangerous areas.
One serious drawback in all type of analyses on a semi-detailed to detailed scale (1:10.000 to 1:2.000) is the fact that two master factors in landslide hazard zonation are very difficult to map in the field. These factors are the depth of the potential failure surface and the groundwater table. The spatial and temporal distribution of the groundwater table can be modelled with hydrologic models. The depth of the potential failure surface should be mapped from existing landslides, taking into account the difference in landslide type.
When all the required data are collected, calculations have to be performed, in which GIS has to be integrated with deterministic models. This can cause problems because GIS is mainly developed for storing, updating, displaying, overlaying and reclassifying data while deterministic models require complex calculation procedures. Full integration of GIS and stability models would require the tedious work of rewriting existing slope stability programs for a GIS environment. However, once these models would be available in GIS, it would be very versatile and much less tedious for successive applications.
![]()
Acknowledgements
Dinand Alkema, Henk Kruse and Marnix Mosselman are thanked for their contribution to the Manizales project.
References
Aldridge R. and Jackson R.J., 1968. Interception of rainfall by Manuka (Leptospermum scoparium) at Taita, New Zealand. New Zealand Journal of Science, 11: 301-317.
Blalock, H.M., 1979. Social statistics, Mac Graw Hill, New York, 625 pp.
De Roo A.P.J., 1993. Modelling surface runoff and soil erosion in catchments using geographical information systems. Nederlanse Geographische Studies 157, Utrecht,295p.
Doorenbos J. and Pruitt W.O., 1984. Guidelines for predicting crop water requirements. FAO Irrigation and Drainage Paper 24. FAO, Rome.
Kirkby M.J., Naden P.S., Burt T.P., and Butcher D.P., 1987. Computer Simulation in Physical Geography. John Wiley, New York, 227 pp.
Mool P.K., 1992. Mass movement susceptibility analysis at the medium scale using a GIS system (ILWIS) applied to an area east of Manizales, Caldas, Colombia. Unpublished Msc thesis, ITC, Enschede, The Netherlands, 140 pp.
Mulder H.F.H.M., 1991. Assessment of landslide hazard. Nederlandse Geographische Studies 124, Utrecht, 150 pp.
Naranjo J.L. and Rios, P.A., 1989. Geologia de Manizales y sus alrededores y su influencia en los riesgos geologicos. Revista Universidad de Caldas, 10, Nos. 1-3, 113 pp. Universidad de Caldas, Manizales, Colombia.
Newmark, N.M. 1965. Effects of Earthquakes on Dams and Embankments. Geotechnique Vol. XV, No. 2.
Okimura, T. and Kawatani, T. 1987. Mapping of the potential surface-failure sites on granite mountain slopes. In: Gardiner (Editor), International Geomorphology. Part 1, John Wiley, New York, pp. 121-138.
Rijtema, P.E., 1965. An analysis of actual evapotranspiration, Agricultural Research Report, Pudoc, Wageningen, 107 pp.
Thornthwaite, C.W. and Mather J.R., 1957. Instructions and tables for computing potential evapotranspiration and the water balance. Climatology, 10, Vol. 3: 185-311.
Van Asch, Th.W.J. and Mulder H.F.H.M., 1988. A stochastical approach to landslide hazard determination in a forested area. Proceedings of the 5th International Symposium on Landslides, Lausanne: 239-244.
Van Asch, Th.W.J. and Mulder, H.F.H.M., 1991. Statistical, geotechnical and hydrological approaches in landslide hazard assessment of mass movements. UNESCO-ITC project on mountain hazard mapping in the Andean environment using Geographical Information Systems. Expert workshop 1991, Bogotá, 31 p.
Van Asch, Th.W.J, Van Westen C.J., Blijenberg H., and Terlien M.T.J., 1992. Quantitative landslide hazard analyses in volcanic ashes of the Chinchina area, Colombia. Proceedings 1er Simposio Internacional sobre Sensores Remotes y Sistemas de Informacion Geografica para el estudio de Riesgos Naturales, Bogotá, Colombia, 10-12 March 1992: 433-443.
Van Asch Th.W.J., 1992. The role of water in landslide hazard analyses. Proceedings 1er symposio international sobre sensores remotos y sistemas de information geografica para el estudio de riesgos naturales, Bogota, Colombia, 10-12 March 1992:485-498.
Van Asch, Th.W.J. and Sukmantalya I.N., 1993. The modelling of soil slip erosion in the Upper Komerin area South Sumatra province, Indonesia. Geografica Phisica (in press).
Van Westen C.J., Van Duren I., Kruse H.M.G., and Terlien M.T.J., 1993. GISSIZ: training package for Geographic Information Systems in Slope Instability Zonation. ITC-Publication Number 15, ITC, Enschede, The Netherlands. Volume 1: Theory, p. 245, Volume 2: Exercises, p. 359, 10 diskettes.
Ward, T.J., Li, R.M. and Simons D.B., 1982. Use of a mathematical model for estimating potential landslide sites in steep forested drainage basins. In: R.T.H. Davies and A.J. Pierce (Editors), Erosion and sedimentation in the Pacific Rim steeplands. . IAHS publ. no 32, pp 21-41.